Trajectoires, mission de type conjonction ou opposition

Nous abordons ici la question du choix de la trajectoire pour rejoindre Mars.

1. Trajectoire de Hohmann

Lorsqu'on lance un vaisseau depuis la Terre, il faut qu'il atteigne la vitesse de libération, soit 11 km/s, pour qu'il échappe à l'attraction terrestre. Cette vitesse doit être atteinte progressivement à partir de l'orbite basse. Ensuite, une fois les ergols épuisés, le vaisseau s'éloigne de la Terre, mais la force d'attraction de notre planète continue de le freiner jusqu'à ce que sa vitesse soit à peine supérieure à 0km/s à environ 1 million de km de la Terre. A cette distance, l'attraction solaire étant plus forte que celle de la Terre, le vaisseau resterait sur une orbite solaire très proche de la Terre. Pour rejoindre Mars, il faut donner au vaisseau en orbite basse une vitesse supérieure à la vitesse de libération, de sorte qu'à 1 million de km de la Terre, la vitesse résiduelle soit suffisante pour changer d'orbite solaire de manière significative et atteindre celle de Mars. La carte des Delta V permet de mieux comprendre combien il faut accélérer les vaisseaux pour atteindre des destinations éloignées.

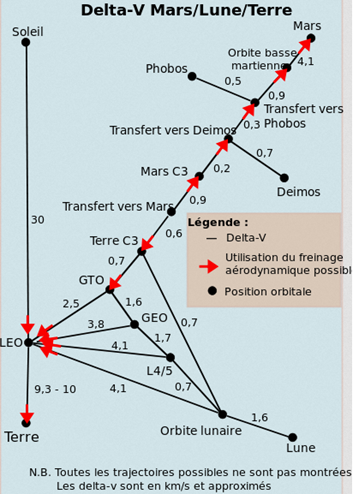
Une fois en orbite basse (LEO = Low Earth Orbit), le vaisseau tourne autour de la Terre à plus de 8km/s, mais il faut encore augmenter la vitesse de 2,5+0,7+0,6=3,8 km/s pour être sur une orbite solaire de transfert vers Mars. En quittant l'attraction terrestre à 1 million de km d'altitude, le différentiel de vitesse par rapport à la Terre n'est que de quelques km/s, mais si on a accélère dans la bonne direction, elle s'ajoute à celle de la Terre autour du soleil (30 km/s) et permet d'atteindre l'orbite martienne. Le vaisseau suit alors une trajectoire dite de Hohmann, la plus économe en ergols. Cette trajectoire est indiquée en jaune ci-dessous, alors que la trajectoire de la Terre est en bleu et celle de Mars en rouge. Pour cette ellipse jaune, le point le plus proche du soleil (périhélie) est la Terre et le plus éloigné (aphélie) est l'orbite martienne.

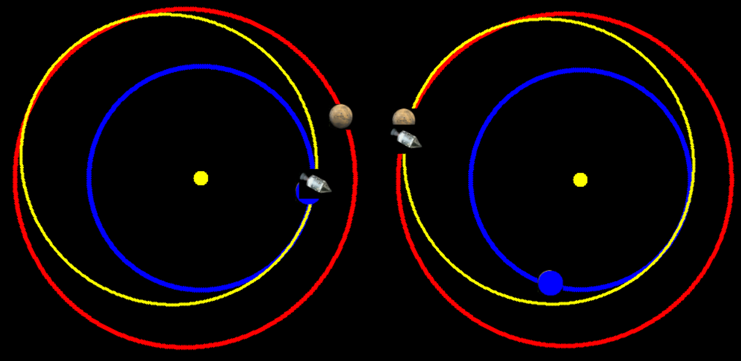
Comme on le voit sur ce schéma avec à gauche la position des planètes et du vaisseau lors du décollage, et à droite la position des planètes et du vaisseau lorsque Mars est atteinte, la Terre a effectué plus d'un demi-tour autour du soleil. Il s'est donc écoulé près de 9 mois. C'est donc la durée approximative du voyage.

Quatre remarques importantes :

• D'abord, il faut viser juste ! Il y a très peu de marge au niveau de la date de départ vers Mars. Il faut attendre une configuration planétaire particulière, avec Mars légèrement devant la Terre, afin que la planète soit à proximité du vaisseau lorsqu'il atteint l'orbite en question. Cette configuration survient tous les 2 ans et 2 mois.
• L'orbite martienne est une ellipse beaucoup plus allongée que celle de la Terre. Il y a donc des configurations plus ou moins favorables selon que Mars est plus ou moins proche du soleil à l'arrivée du vaisseau.
• Un autre paramètre important de la trajectoire est la différence angulaire entre les plans orbitaux solaires de la Terre et Mars. Par chance, les deux planètes orbitent presque dans le même plan. Cette différence angulaire a cependant un léger impact sur la direction visée et donc sur la quantité d'ergols embarquée, en fonction de la configuration planétaire au moment du départ vers Mars.
• Pour le retour, le problème est symétrique : il faut attendre la bonne configuration planétaire pour revenir vers la Terre selon une trajectoire de Hohmann. En conséquence, les astronautes doivent rester sur Mars pendant environ 1 an et demi ! Puis le retour dure également environ 9 mois.

2. Mission de type conjonction

On parle de conjonction d'une planète lorsqu'elle se trouve relativement proche du soleil pour un observateur situé sur Terre (on les voit dans la même zone du ciel). Une mission est donc de type conjonction lorsque le décollage a lieu dans de telles circonstance. Une trajectoire de Hohmann, minimaliste en énergie, peut être choisie pour ce type de mission. On peut aussi choisir d'accélérer un peu ou de jouer sur la date du décollage. Le problème, toutefois, c'est qu'une fois arrivés sur Mars, les astronautes doivent attendre près de 500 jours la conjonction suivante entre les 2 planètes pour pouvoir repartir sur une trajectoire symétrique économe en énergie. Voir schéma ci-dessous (tiré du rapport DRA 5.0).

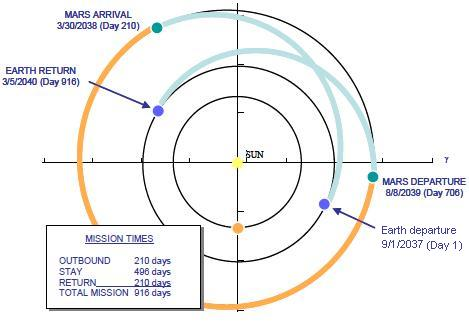
3. Mission de type opposition

Une mission vers Mars est de type opposition lorsque le retour (ou l'aller) a lieu quand Mars et le soleil sont opposés dans le ciel vu de la Terre. En vérité, si le soleil est à l'opposé de Mars, cela veut dire que Mars est proche de la Terre. Le problème, c'est que la Terre se déplace sur son orbite beaucoup plus vite que Mars. Et donc, si une fusée décolle à ce moment là d'une planète pour rejoindre l'autre, 6 mois plus tard, les planètes se sont beaucoup éloignées et le vaisseau n'est pas prêt d'arriver. La solution du scénario d'opposition est soit d'aller beaucoup beaucoup plus vite pour atteindre la Terre avant qu'elle ne se soit éloignée, soit d'aller jusqu'à Vénus et de réaliser un mouvement de balancier pour revenir jusqu'à la Terre ... après un très long voyage. Malgré tout, l'intérêt de ce type de mission est de pouvoir réduire considérablement la durée du séjour sur Mars, typiquement 1 à 2 mois. Un schéma classique du scénario d'opposition est présenté ci-dessous (tiré également du scénario NASA de 2009).

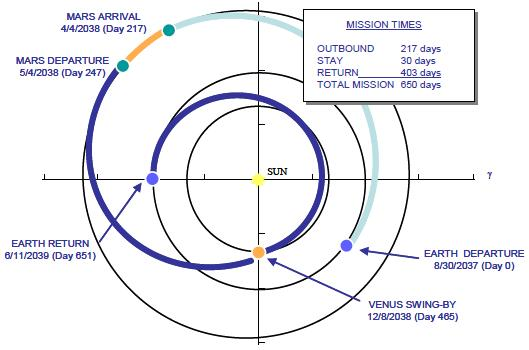
4. Comparaison énergétique des 2 types de mission

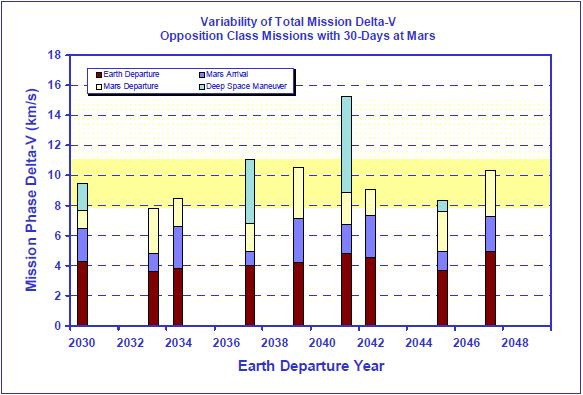
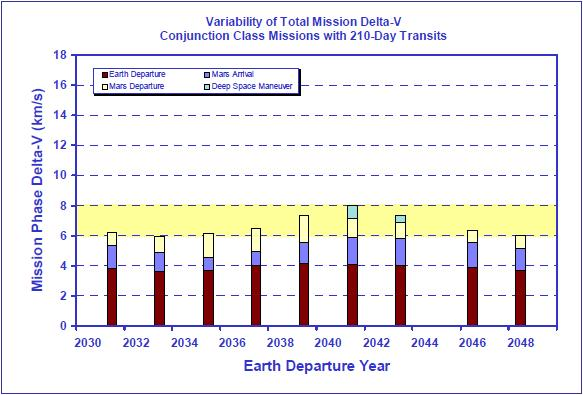
En astronautique, le nerf de la guerre si on peut dire, c'est la masse totale de ce qu'il faut envoyer dans l'espace, car c'est elle qui conditionne le nombre de fusées géantes qu'il faut faire décoller et la complexité de la procédure d'assemblage en orbite basse. Rappelons que dans le document NASA DRA 5.0, 9 fusées géantes sont nécessaires à la mission, avec des risques d'échec très importants. Or, ce sont les ergols qui constituent la plus grande partie de cette masse et de loin. Et la quantité d'ergols nécessaire est directement liée aux besoins énergétiques, qui peut s'exprimer en "delta V", c'est-à-dire en nombre de km/s qu'il faut gagner à chaque phase de la mission. Voici ci-dessous (extrait du rapport NASA) un bilan des besoins en fonction de la date de départ de la mission. Cela varie en effet fortement en fonction de la position de Vénus et du contexte de rapprochement de Mars par rapport à la Terre (Mars a une trajectoire elliptique excentrée autour du soleil). Comme on peut le voir, les missions de type conjonction minimisent les besoins énergétiques et donc la masse des ergols. Bien entendu, une mission plus longue sur Mars nécessiterait plus de consommables, mais cette masse additionnelle ne serait rien en comparaison de la masse additionnelle des ergols si on choisit une mission de type opposition. Sur le plan massique, donc, c'est la mission de type conjonction qui est incontestablement plus efficace.

Conclusion

La plupart des scénarios proposés par les spécialistes sont basés sur des missions de type conjonction, avec une trajectoire proche de Hohmann et une durée globale de la mission de l'ordre de 3 ans.

... Envie de lire la suite ?

Cet article est disponible dans sa version complète pour les membres APM avec une cotisation à jour.

Déjà membre ? Me connecter. Sinon, devenez membre aujourd'hui et ne ratez aucune info sur Mars !

Si vous avez déjà été membre, rendez-vous sur la page Mon Compte pour renouveler votre cotisation.